در موضوع عیبیابی ماشینهای دوار، استفاده از سیگنالهای ارتعاشی نظیر شتاب، سرعت و جابجایی از آنرو که این سیگنالها حاوی اطلاعات دینامیکی از وضعیت ماشین میباشند؛ در شناسایی و تمایز بین عیوب گوناگون موثر است. روشهای تحلیل و تشخیص عیب در ماشینهای دوار به کمک سیگنالهای ارتعاشی میتواند به سه دسته زیر تقسیم بندی شود:
تحلیلهای حوزه زمان مستقیما مبتنی بر شکل موج زمانی است. تحلیلهای سنتی حوزه زمان ویژگیهای مشخصهای را به صورت توصیفات آماری از سیگنالهای شکل موج زمانی محاسبه میکند. ویژگیهایی نظیر میانگین، قله، ضریب کرست، و آمارهای مرتبه بالا نظیر root mean square، skewness، kortosis و غیره. این گونه ویژگیها که عمدتا ویژگیهای حوزه زمان نامیده میشود با تواناییهای محدود در شناسایی عیوب محلی بکار گرفته شدهاند. رویکردهای تحلیلی رایج حوزه زمان نظیر میانگینگیری همزمان، و مدل خود برگشت کننده، به صورت گستردهای برای عیبیابی ماشینهای دوار استفاده میگردد.
تحلیلهای حوزه فرکانس یا تحلیل طیفی عموما به وسیله تبدیل فوریه انجام میگیرد. تحلیل فوریه یک سیگنال حوزه زمان f(t) را به حوزه فرکانس تبدیل میکند؛ به گونه ای که طیف تولید شده F(ω) شامل کلیه محتوای فرکانسی سیگنال (پایهای و هارمونیک) که به صورت رابطه زیر تعریف میشود:
اما مهمترین نقص FFT عدم توانایی آن در ارائه اطلاعاتی راجع به شرایط زمانی طیف سیگنال تحلیل شده است؛ به طوری که نتایج آن به صورت میانگینی بر کل بازه سیگنال است. این موضوع در تحلیل سیگنالهای غیرایستا مشکل آفرین خواهد شد. در چنین مواردی داشتن ارتباط مابین زمان و محتوای فرکانسی سیگنال میتواند مفید باشد. این محدودیت جدی FFT منجر به بکارگیری ابزارهای تحلیل سیگنال زمان-فرکانس نظیر “تبدیل فوریه زمان کوتاه” (STFT)، یا “توزیع وینگر وایل” (WVD) و غیره شد. روش STFT یک سیگنال را به یک تابع دو بعدی زمان و فرکانس تصویر میکند. تبدیل فوریه زمان کوتاه یا همان STFT با بکار گیری یک تابع پنجره لغزان g(t) به مرکزیت زمانی τ، یک تبدیل فوریه “time-localized” بر روی سیگنال x(t) به صورت پی در پی، انجام میدهد. در نتیجه تغییرات محتوای فرکانسی سیگنالی که درون تابع پنجره زمانی قرار گرفته ظاهر میشود. در شکل زیر این فرآیند دیده میشود:
1) Time-synchronous averaging
2) Autoregressive model
3) Winger-Ville Distribution (WVD)
مشکل در استفاده از STFT آن است که، دقت آن در استخراج محتوای فرکانسی به وسیله طول پنجره نسبت به بازه سیگنال، محدود میشود. وقتی تابع پنجره تعریف میشود، مساحت تابع پنجره (حاصل زمان درپهنای باند) در صفحه زمان- فرکانس، ثابت میماند. این بدان معناست که تفکیک زمان و تفکیک فرکانس به طور همزمان افزایش نمییابد. لذا در STFT مصالحهای بین تفکیک زمانی و فرکانسی وجود دارد.
در تحلیلهای حوزه زمان- فرکانس تبدیل موجک روشی نسبتا جدید و ابزاری قدرتمند در زمینه تحلیل سیگنال است که توانسته بر محدودیت های سایر روشها – علیالخصوص در تحلیل سیگنالهای غیر ایستا- غلبه کند. این تبدیل امکان استفاده از بازههای زمانی طولانی را که در آن اطلاعات فرکانس پایین به صورت دقیق تر مطلوب است؛ فراهم میکند. همچنین میتوان از بازههای زمانی کوتاهتر که در آن اطلاعات فرکانس بالای دقیق مطلوب است؛ استفاده کرد. همچنین این تبدیل در استخراج سیگنالهای با پهنای باند باریک فرکانسی بکار گرفته میشود. مهمترین مزیت استفاده از موجک توانایی آن در تحلیل محلی یک سیگنال و یا تمرکز بر هر بازه زمانی بدون از دست دادن اطلاعات طیفی موجود در سیگنال است. از این رو تحلیل موجک میتواند برخی جنبههای داده را که تکنیکهای تحلیلی قدیمی قادر به یافتن آن نیستند، ظاهر کند. این ویژگی علیالخصوص جهت کشف عیوب و یا آسیبهایی نظیر ترک بسیار مهم است.
در مقایسه با روش STFT که در آن اندازه پنجره ثابت است، تبدیل موجک امکان تغییر اندازه پنجره را در تحلیل ترکیبات مختلف فرکانسی در یک سیگنال فراهم میکند. این موضوع با مقایسه سیگنال، با مجموعهای از توابع که از اتساع و انقباض و انتقال (انتقال در زمان) یک موجک پایه (t)ψ به دست آمده؛ و یافتن شباهتهای آنها، حاصل میشود. در شکل زیر این فرآیند دیده میشود:
1) Scaling
2) Shifting
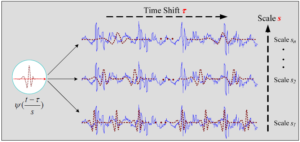
فرآیندهای scaling و shifting یک موجک پایه بر روی سیگنال
تبدیل موجک به سه صورت زیر انجام میشود:
تبدیل موجک پیوسته (CWT)
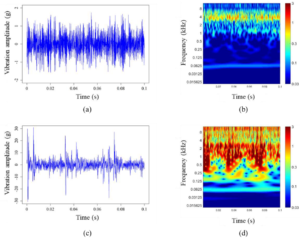
تبدیل موجک گسسته (DWT)
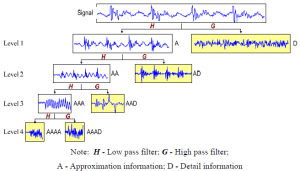
تبدیل به وسیله بسته های موجک (WPD)
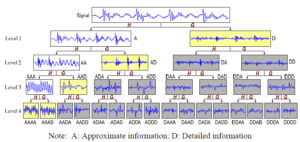
يکي از روش هايي که در حال حاضر به صورت گسترده براي مسئله طبقه بندی مورد استفاده قرار ميگيرد، روش ماشين بردار پشتيبان (SVM) است. شايد بتوان محبوبيت کنوني روش ماشين بردار پشتيبان را با محبوبيت شبکههاي عصبي در دهه گذشته مقايسه کرد. اين روش از جمله روشهاي نسبتاً جديدي است که در سالهاي اخير کارايي بهتری نسبت به روشهاي قديميتر طبقهبندي از جمله شبکههاي عصبي پرسپترون، از خود نشان داده است. مبناي کاري دستهبندي کننده SVM دستهبندي خطي دادهها است و در تقسيم خطي دادهها سعي ميکند خط یا به طور کلی اَبَرصفحه ای را انتخاب کند که حاشيه اطمينان بيشتري داشته باشد. این موضوع در شکل زیر دیده میشود. حل معادلة پيدا کردن خط بهينه براي دادهها به وسيله روشهاي برنامه سازی درجه دوم یا QP که از روشهاي شناخته شده در حل مسائل مقید هستند صورت ميگيرد. روش SVM از يک تکنيک که لم هسته ناميده مي شود، براي تبديل دادهها استفاده ميکند و بر اساس اين تبديل، مرز بهينه بين خروجيهاي ممکن را پيدا ميکند. به عبارت ساده تبديلات بسيار پيچيده را انجام داده، سپس مشخص ميکند چگونه دادهها بر اساس برچسبها يا خروجيهای تعريف شده، جدا شوند.
1) Classification
2) Hyper Plane
3) Quadratic Programming (QP)
4) Kernel trick
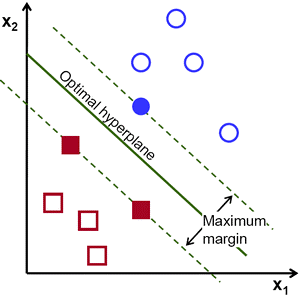
یافتن بهترین اَبَرصفحه که از دو دسته داده بیشترین فاصله را داشته باشد توسط svm
روشن است که سیگنال بدون نویز در جهان خارج وجود ندارد. نویزهای ذاتیاز قبیل نویز سفید، نویز شلیکی، نویز پراکندگی و نویزهای عارضی نظیر اغتشاشات محیطی و نویزهای مکالمه متقابل، دو منبع غیر قابل اجتناب نویز میباشند. لذا حذف نویز یکی از مراحل پایهای و اصلی در پردازش سیگنال به شمار میرود. اما هنگامی که عیوب نوزاد و نادر در یک سیگنال جستجو میشوند، حذف نویز امری جدی و حساس خواهد بود.
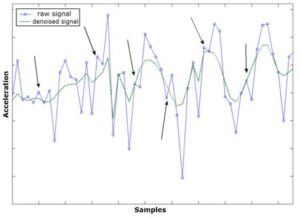
امروزه تبديل موجك به يكي از مهمترين ابزارها در زمينه تحليلهاي عددي و پردازش سيگنال و تصوير تبديل شده است. با توجه به خواص تبديل موجك، كارآيي اين تبديل در حذف نويز نيز به اثبات رسيده است. هدف اصلي در حذف نويز اين است كه سيگنال بازسازي شده تا حد امكان به سيگنال اصلي نزديك بوده و در عين حال خواص اصلي سيگنال چون ميزان همواري آن نيز حفظ شود.
1) Intrinsic
2) Shot noise
3) Diffusion noise
4) Extrinsic noise
5) Crosstalk noise
کشف نوظهوری یا همان novelty detection برای اولین بار در ایران در سال ۱۳۹۵ در رساله دکتری آقای محمدصالح صدوقی در دانشگاه تربیت مدرس معرفی شد (حدود ۲۰ سال پیش از آن در دانشگاههای خارج از کشور مطرح شده بود).
کشف نوظهوری به معنای شناخت انحراف داده های تست- از جنبههای گوناگون- نسبت به الگوی دادههای در دسترس در مرحله تعلیم است. اهمیت کاربردی و ماهیت چالشی این روش منجر به ارائه رویکردهای مختلفی شده است. این روشها عموما بر مجموعه داده هایی اعمال شده است که مقادیر زیادی از نمونه های حالت نرمال سیستم در دسترس بوده ولی نمونه های حالت غیرنرمال به مقدار کافی وجود نداشته است. در ادامه روشهای مختلف اجرا شده در مبحث کشف نوظهوری ارائه میشود.
در شکلهای زیر شماتیکی از مفهوم کشف نوظهوری دیده میشود. در شکل دوم به دور فضای حالت نرمال که توسط دادههای نرمال فرض شده ایجاد شده است، مرزی رسم شده است و دادهای که خارج از این مرز قرار گفته به عنوان داده غیرنرمال معرفی شده است.
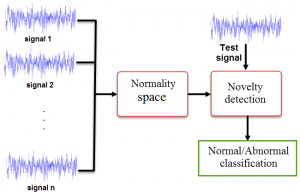
خلاصه روش کشف نوظهوری
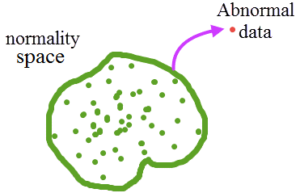
شماتیکی از مفهوم روش کشف نوظهوری در فضای دو بعدی


تهران، خیابان کارگر شمالی، پارک علم و فناوری دانشگاه تربیت مدرس، طبقه سوم، واحد ۳۰۱
vibromodares@gmail.com
info@vibromodares.com
